Моделирование распределения тепловых напряжений, возникающих при радиационном облучении

УДК 539.376

Моделирование распределения тепловых напряжений, возникающих при радиационном облучении

В.К.Зольников¹, И.В. Семейкин²

¹ ФГБОУ ВО «Воронежский государственный лесотехнический университет имени Г.Ф.Морозова»

²АО «Научно-исследовательский институт электронной техники»

Аннотация: в статьерассматриваются теоретические аспекты моделирования тепловых напряжений под действием облучения и предлагаются возможные подходы решения в традиционном классе скалярных функций детерминированных начально-краевых задач распределения динамических напряжений с постоянными теплофизическими характеристиками.

Ключевые слова: термические напряжения, изотермические деформации, неоднородная начально-краевая задача на полуоси.

MODELING OF THE DISTRIBUTION OF THERMAL STRESSES ARISING UNDER RADIATION IRRADIATION

V.K. Zolnikov¹, I.V. Semeikin²

¹Voronezh State University of Forestry and Technologies named after G.F. Morozov

² JSC«Scientific Research Institute of Electronic»

Abstract: Theoretical aspects of modeling thermal stresses under irradiation are considered, and possible solution approaches are proposed within the traditional class of scalar functions for deterministic initial-boundary value problems of dynamic stress distribution with constant thermophysical characteristics.

Keywords: thermal stresses, isothermal deformations, nonhomogeneous initial-boundary value problem on a half-line.

I. Теоретические аспекты распределения напряжений в упругом полупространстве, возникающих при облучении

Рассматривается упругое полупространство, занимающее область х ≥ 0. Его начальная температура постоянна и равна Т₀ [1]. Пусть поверхность полупространства подвергается облучению с удельной мощностью q (x,t). В результате облучения температура полупространства будет увеличиваться, причем наибольшему нагреву будут подвергаться поверхностные слои.

Вследствие интенсивного облучения температура поверхностного слоя может резко увеличиться. Кроме того, поверхностный слой подвержен наибольшему радиационному повреждению. Часть поверхностных атомов испаряется, образуя конденсат. Пусть температура образовавшегося конденсата из поверхностных атомов резко повысилась до значения θ. Тогда между конденсатом и поверхностью упругого полупространства х = 0 будет происходить конвективный теплообмен с заданным коэффициентом теплоотдачи α.

Математическая формулировка сделанных предположений приводит к следующей постановке задачи:

нестационарное распределение температуры Т(х,t) полупространства будет определяться как решение неоднородного уравнения теплопроводности:

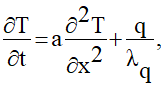
(1.1)

где а — коэффициент температуропроводности упругого полупространства, λ_q — коэффициент его теплопроводности и q — удельная мощность источников тепла.

Также распределение температуры Т(х,t) должно подчиняться начальному условию:

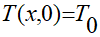(1.2)

и граничному условию на поверхности полупространства х = 0:

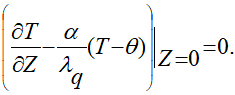(1.3)

Таким образом, распределение температуры в упругом полупространстве определяется как решение неоднородной начально-краевой задачи (1.1) — (1.3) на полуоси с краевым условием третьего рода.

Распределение динамических напряжений [1], в предположении отсутствия поверхностных сил, определяется как решение уравнения:

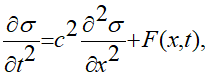(1.4)

где 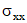— компонента тензора напряжений; 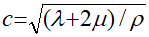— скорость продольных волн; ρ — плотность материала; λ, μ — коэффициенты Ляме при изотермической деформации, а функция F определяется выражением:

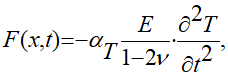(1.5)

где α_Т — коэффициент линейного расширения; 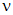— коэффициент Пуассона; Е — модуль упругости.

Так как в начальный момент времени термических напряжений не было, то распределение напряжений в полупространстве подчиняется однородным начальным условиям:

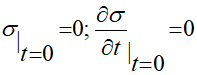(1.6)

В предположении отсутствия поверхностных сил

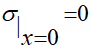(1.7)

Таким образом, распределение динамических напряжений в упругом полупространстве определяется как решение неоднородной начально-краевой задачи (1.4) — (1.7) на полуоси с краевым условием первого рода.

Другие компоненты тензора напряжений связаны с σ предлагаемыми в библиографическом источнике [1] выражениями:

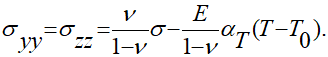(1.8)

Решение начально-краевой задачи (1.1) — (1.3) представляют [1] в виде:

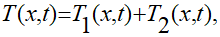(1.9)

где функция Т₁(х,t) является решением соответствующего однородного уравнения теплопроводности, то есть уравнения (1.1) при q = 0 с условиями (1.2) и (1.3), а функция Т₂(х,t) является решением неоднородного уравнения теплопроводности (1.1) с однородными условиями (1.2) и (1.3), то есть при Т₀ = 0 в (1.2) и θ = 0 в (1.3).

Для функции Т₁(х,t) приводят следующее выражение:

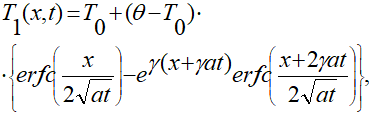(1.10)

где γ = α/λ_q, 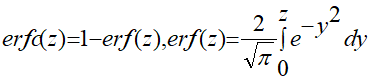– интеграл ошибок.

Выражение (1.10) описывает температурное поле в упругом полупространстве, возникающее за счет конвективного теплообмена у поверхности.

Температурное поле в упругом полупространстве, возникающее за счет облучения, описывается функцией Т₂(х,t), которую записывают в виде [1]:

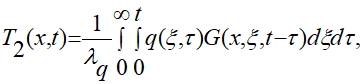(1.11)

где G — функция Грина соответствующей задачи. Для нее получается возможным [1] выражение вида:

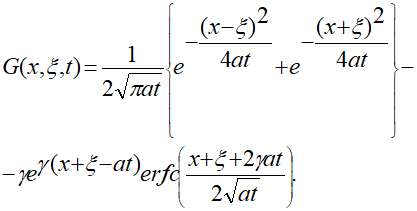(1.12)

Таким образом, представив (1.12) в (1.11), (1.10) и (1.11) в (1.9) получают решение начально-краевой задачи (1.1) — (1.3), описывающее температурное поле, которое возникает в упругом полупространстве за счет облучения с учетом конвективного теплообмена на облучаемой поверхности.

Решение динамической начально-краевой задачи (1.4) — (1.7) получают [1] в таком виде:

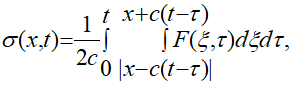(1.13)

где функция F вычисляется по формуле (1.5), куда вставляется найденное температурное поле (1.9).

Предлагается вариант вещественного уравнения распределения динамических напряжений в предположении решения начально-краевой задачи (1.1) — (1.3), сформированное аналитическими функциями рассматривать таким:

(1.14)

Решение рассматриваемого вещественного уравнения распределения динамических напряжений (1.14) в упругом полупространстве при соблюдении возможных начально-краевых условий (1.6) — (1.7) предлагается сформированным аналитическими функциями так:

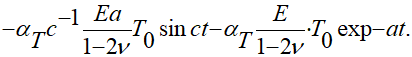(1.15)

При соблюдении действительного варианта решения уравнения (1.1) такого вида

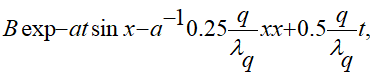(1.16),

записанного аналитическими функциями с последующим учетом начально-краевых условий (1.2) — (1.3) предлагаемое вещественное скалярное уравнение распределения динамических напряжений в упругом полупространстве, возникающих при облучении, рассматривается в следующем виде:

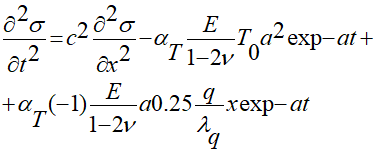(1.17),

вариант решения которого с учетом начально-краевых условий (1.6) – (1.7) разработан таким:

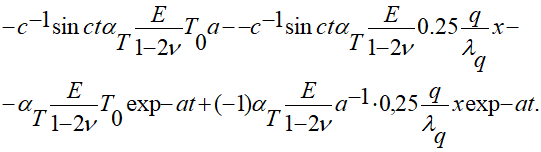(1.18)

II. Вариант решения неоднородной начально-краевой задачи распределения динамических напряжений в упругом полупространстве при детерминированных тепловых источников

В библиографическом источнике [1] рассматривается задача, когда излучение поглощается в упругом полупространстве по экспоненциальному закону, описываемому функцией вида:

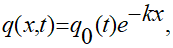(2.1)

где k — коэффициент поглощения энергии падающего излучения;

q₀(t) — удельная мощность источников тепла, возникающего на поверхности упругого полупространства за время облучения t.

Включив (2.1) в (1.11), проводят интегрирование по пространственной координате и получают выражение для Т₂(х,t):

(2.2)

где

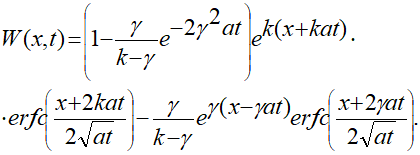(2.3)

С учетом (1.10), (2.2), включаемых в формулу (1.9), получают температурное распределение, возникающее в упругом полупространстве за счет конвективного теплообмена и облучения, интенсивность которого спадает по экспоненциальному закону (2.1).

Затем включают полученное выражение распределения температурного поля в (1.13) для определения распределения создаваемых в этом случае напряжений…. В настоящей работе предлагается вещественное уравнение распределения динамических напряжений в предположении решения вещественной начально-краевой задачи (1.1), (1.2), (1.3) с детерминированным источником тепла :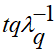

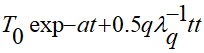(2.4)

рассматривать как:

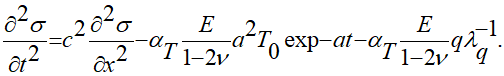(2.5)

Предлагаемый вариант решения аналитическими функциями записанного вещественного уравнения (2.5) с начально-краевыми условиями (1.6), (1.7) разработан так:

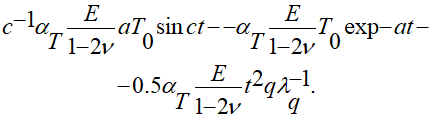(2.6)

С другой стороны, при соблюдении возможных соотношений для начально-краевой задачи (1.1), (1.2), (1.3)

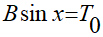
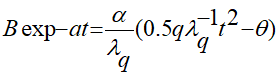
вариант полученного решения оговариваемой задачи записан так:

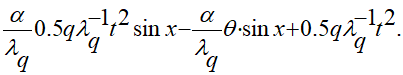(2.7)

Рассматриваемый вариант вещественного уравнения распределения динамических напряжений в упругом полупространстве представляется таким:

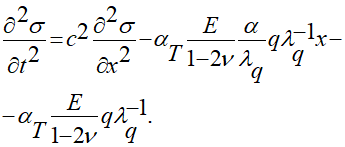(2.8)

Тогда действительный вариант решения аналитическими функциями начально-краевой задачи распределения в исследуемом случае динамических напряжений с начальными и граничными условиями (1.6) — (1.7) разработан так:

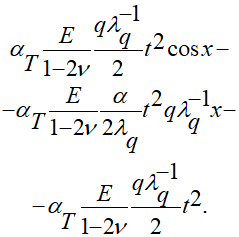
III. Вопросы моделирования распределения напряжений в упругом слое, возникающих при облучении

Уравнения (1.1), (1.2), (1.3) остаются прежними. К ним добавляется условие теплоизоляции на втором конце упругого слоя [1], соответствующее отсутствию теплового потока при x = h:

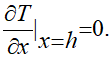(3.1)

В результате для определения температурного поля возникает начально-краевая задача (1.1) — (1.3), (3.1) смешанного типа: на одной границе задано неоднородное условие третьего рода (1.3), а на другой — однородное второго рода (3.1).

Решение такой задачи представляют в виде (1.9), где теперь Т₁(х,t) определяется выражением:

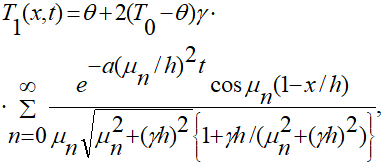(3.2)

где μ_n являются корнями уравнения:

(3.3)

Выражение (3.2) описывает температурное поле в упругом слое, возникающее за счет конвективного теплообмена с конденсатом облучаемой поверхности.

Температурное поле в упругом слое, возникающее за счет облучения, описывается функцией Т₂(х,t), для которой можно получить [1] выражение:

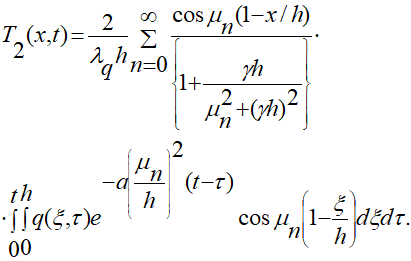(3.4)

Для определения распределения динамических напряжений в упругом слое к постановке начально-краевой задачи (1.4) — (1.7) добавляется краевое условие на второй границе при х = h [1]:

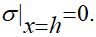(3.5)

Тогда для нахождения напряжения в слое получается начально-краевая задача (1.4) — (1.7), (3.5) с краевыми условиями первого рода. Ее решение получают [1] в виде:

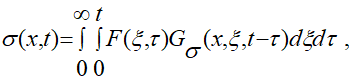(3.6)

где функция Грина соответствующей задачи (1.4) — (1.7), (3.5) определяется выражением:

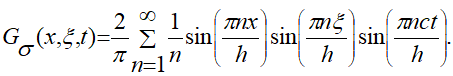(3.7)

В формулу (3.6) включается функция F, вычисляемая по формуле (1.5) с учетом найденного температурного поля (1.9), определяемого выражениями (3.2) и (3.4).

При получении разработанного вещественного решения в аналитическом виде уравнения (1.1) с постоянными теплофизическими характеристиками предлагаемый вариант решения оговариваемой начально-краевой задачи распространения тепла с фиксированным тепловым источником 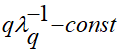, краевыми условиями (1.2), (1.3) с учетом граничного условия теплоизоляции для упругого слоя:

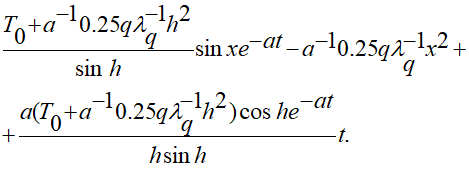(3.8)

Уравнение распределения динамических напряжений в упругом слое исследуется таким:

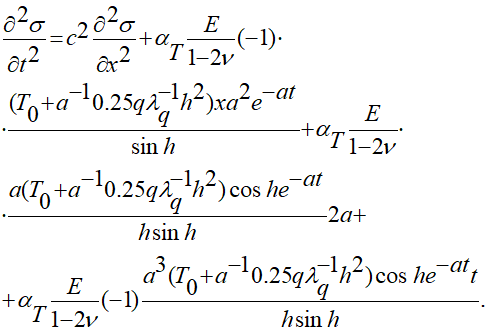(3.9)

Для определения динамических напряжений в упругом слое к начально-краевой задаче (3.9), (1.5), (1.6), (1.7) добавляется краевое условие (3.5).

Вариант вещественного решения такой задачи в аналитическом виде предлагается разработанным так:

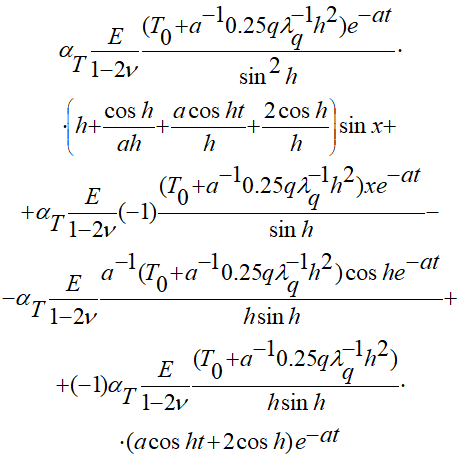(3.10)

При выполнении системы записанных соотношений вида:

(3.11)

возможный вариант решения в аналитическом виде оговариваемой задачи распределения динамических напряжений в упругом слое предлагается сформированным так:

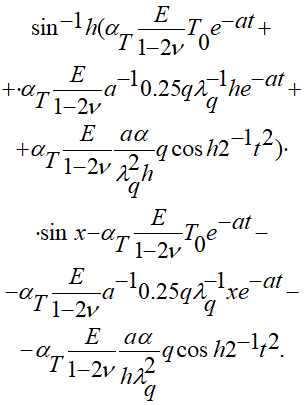(3.12)

Вариант вещественного уравнения распределения динамических напряжений в упругом слое с детерминированным тепловым источником вида 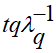предлагается таким:

(3.13)

Возможный вариант действительного решения в аналитическом виде искомой начально-краевой задачи (3.13), (1.5), (1.6), (1.7) с вещественным краевым условием (3.5) предлагается сформированным так:

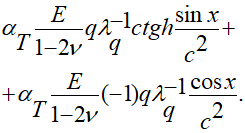(3.14)

I. Теоретические аспекты распределения напряжений в упругом полупространстве, возникающих при облучении

Рассматривается упругое полупространство, занимающее область х ≥ 0. Его начальная температура постоянна и равна Т₀ [1]. Пусть поверхность полупространства подвергается облучению с удельной мощностью q (x,t). В результате облучения температура полупространства будет увеличиваться, причем наибольшему нагреву будут подвергаться поверхностные слои.

Вследствие интенсивного облучения температура поверхностного слоя может резко увеличиться. Кроме того, поверхностный слой подвержен наибольшему радиационному повреждению. Часть поверхностных атомов испаряется, образуя конденсат. Пусть температура образовавшегося конденсата из поверхностных атомов резко повысилась до значения θ. Тогда между конденсатом и поверхностью упругого полупространства х = 0 будет происходить конвективный теплообмен с заданным коэффициентом теплоотдачи α.

Математическая формулировка сделанных предположений приводит к следующей постановке задачи:

нестационарное распределение температуры Т(х,t) полупространства будет определяться как решение неоднородного уравнения теплопроводности:

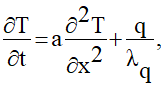
(1.1)

где а — коэффициент температуропроводности упругого полупространства, λ_q — коэффициент его теплопроводности и q — удельная мощность источников тепла.

Также распределение температуры Т(х,t) должно подчиняться начальному условию:

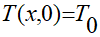(1.2)

и граничному условию на поверхности полупространства х = 0:

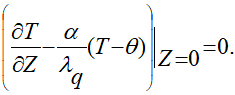(1.3)

Таким образом, распределение температуры в упругом полупространстве определяется как решение неоднородной начально-краевой задачи (1.1) — (1.3) на полуоси с краевым условием третьего рода.

Распределение динамических напряжений [1], в предположении отсутствия поверхностных сил, определяется как решение уравнения:

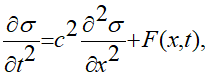(1.4)

где 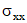— компонента тензора напряжений; 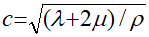— скорость продольных волн; ρ — плотность материала; λ, μ — коэффициенты Ляме при изотермической деформации, а функция F определяется выражением:

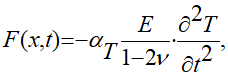(1.5)

где α_Т — коэффициент линейного расширения; 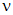— коэффициент Пуассона; Е — модуль упругости.

Так как в начальный момент времени термических напряжений не было, то распределение напряжений в полупространстве подчиняется однородным начальным условиям:

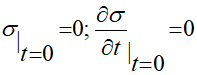(1.6)

В предположении отсутствия поверхностных сил

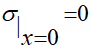(1.7)

Таким образом, распределение динамических напряжений в упругом полупространстве определяется как решение неоднородной начально-краевой задачи (1.4) — (1.7) на полуоси с краевым условием первого рода.

Другие компоненты тензора напряжений связаны с σ предлагаемыми в библиографическом источнике [1] выражениями:

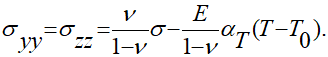(1.8)

Решение начально-краевой задачи (1.1) — (1.3) представляют [1] в виде:

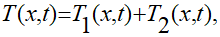(1.9)

где функция Т₁(х,t) является решением соответствующего однородного уравнения теплопроводности, то есть уравнения (1.1) при q = 0 с условиями (1.2) и (1.3), а функция Т₂(х,t) является решением неоднородного уравнения теплопроводности (1.1) с однородными условиями (1.2) и (1.3), то есть при Т₀ = 0 в (1.2) и θ = 0 в (1.3).

Для функции Т₁(х,t) приводят следующее выражение:

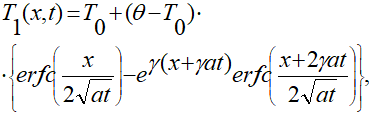(1.10)

где γ = α/λ_q, 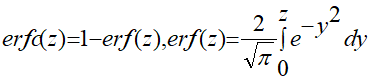– интеграл ошибок.

Выражение (1.10) описывает температурное поле в упругом полупространстве, возникающее за счет конвективного теплообмена у поверхности.

Температурное поле в упругом полупространстве, возникающее за счет облучения, описывается функцией Т₂(х,t), которую записывают в виде [1]:

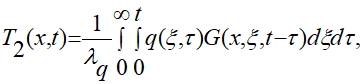(1.11)

где G — функция Грина соответствующей задачи. Для нее получается возможным [1] выражение вида:

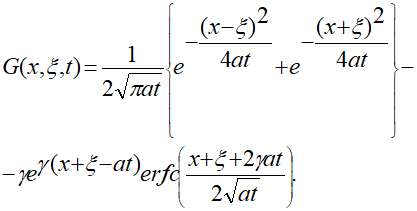(1.12)

Таким образом, представив (1.12) в (1.11), (1.10) и (1.11) в (1.9) получают решение начально-краевой задачи (1.1) — (1.3), описывающее температурное поле, которое возникает в упругом полупространстве за счет облучения с учетом конвективного теплообмена на облучаемой поверхности.

Решение динамической начально-краевой задачи (1.4) — (1.7) получают [1] в таком виде:

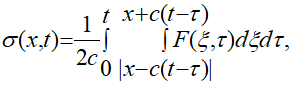(1.13)

где функция F вычисляется по формуле (1.5), куда вставляется найденное температурное поле (1.9).

Предлагается вариант вещественного уравнения распределения динамических напряжений в предположении решения начально-краевой задачи (1.1) — (1.3), сформированное аналитическими функциями рассматривать таким:

(1.14)

Решение рассматриваемого вещественного уравнения распределения динамических напряжений (1.14) в упругом полупространстве при соблюдении возможных начально-краевых условий (1.6) — (1.7) предлагается сформированным аналитическими функциями так:

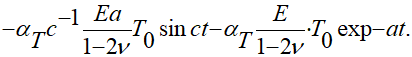(1.15)

При соблюдении действительного варианта решения уравнения (1.1) такого вида

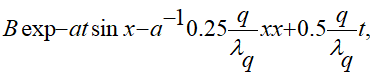(1.16),

записанного аналитическими функциями с последующим учетом начально-краевых условий (1.2) — (1.3) предлагаемое вещественное скалярное уравнение распределения динамических напряжений в упругом полупространстве, возникающих при облучении, рассматривается в следующем виде:

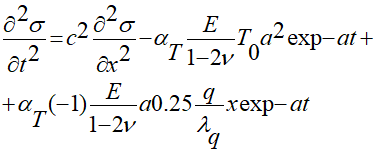(1.17),

вариант решения которого с учетом начально-краевых условий (1.6) – (1.7) разработан таким:

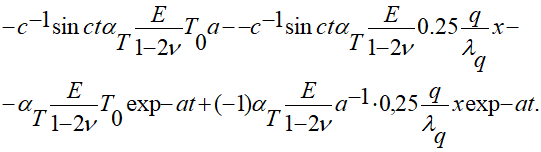(1.18)

II. Вариант решения неоднородной начально-краевой задачи распределения динамических напряжений в упругом полупространстве при детерминированных тепловых источников

В библиографическом источнике [1] рассматривается задача, когда излучение поглощается в упругом полупространстве по экспоненциальному закону, описываемому функцией вида:

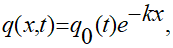(2.1)

где k — коэффициент поглощения энергии падающего излучения;

q₀(t) — удельная мощность источников тепла, возникающего на поверхности упругого полупространства за время облучения t.

Включив (2.1) в (1.11), проводят интегрирование по пространственной координате и получают выражение для Т₂(х,t):

(2.2)

где

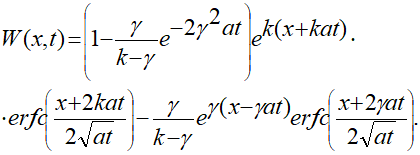(2.3)

С учетом (1.10), (2.2), включаемых в формулу (1.9), получают температурное распределение, возникающее в упругом полупространстве за счет конвективного теплообмена и облучения, интенсивность которого спадает по экспоненциальному закону (2.1).

Затем включают полученное выражение распределения температурного поля в (1.13) для определения распределения создаваемых в этом случае напряжений…. В настоящей работе предлагается вещественное уравнение распределения динамических напряжений в предположении решения вещественной начально-краевой задачи (1.1), (1.2), (1.3) с детерминированным источником тепла :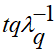

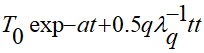(2.4)

рассматривать как:

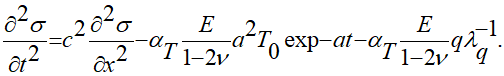(2.5)

Предлагаемый вариант решения аналитическими функциями записанного вещественного уравнения (2.5) с начально-краевыми условиями (1.6), (1.7) разработан так:

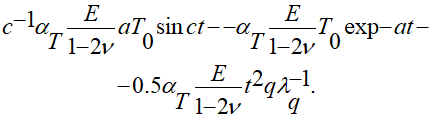(2.6)

С другой стороны, при соблюдении возможных соотношений для начально-краевой задачи (1.1), (1.2), (1.3)

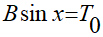
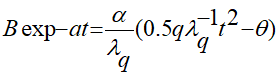
вариант полученного решения оговариваемой задачи записан так:

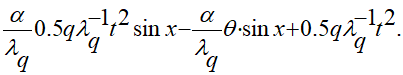(2.7)

Рассматриваемый вариант вещественного уравнения распределения динамических напряжений в упругом полупространстве представляется таким:

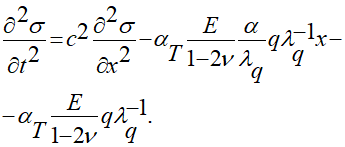(2.8)

Тогда действительный вариант решения аналитическими функциями начально-краевой задачи распределения в исследуемом случае динамических напряжений с начальными и граничными условиями (1.6) — (1.7) разработан так:

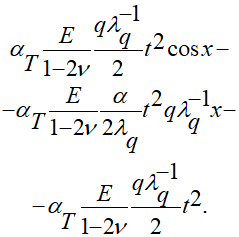
III. Вопросы моделирования распределения напряжений в упругом слое, возникающих при облучении

Уравнения (1.1), (1.2), (1.3) остаются прежними. К ним добавляется условие теплоизоляции на втором конце упругого слоя [1], соответствующее отсутствию теплового потока при x = h:

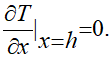(3.1)

В результате для определения температурного поля возникает начально-краевая задача (1.1) — (1.3), (3.1) смешанного типа: на одной границе задано неоднородное условие третьего рода (1.3), а на другой — однородное второго рода (3.1).

Решение такой задачи представляют в виде (1.9), где теперь Т₁(х,t) определяется выражением:

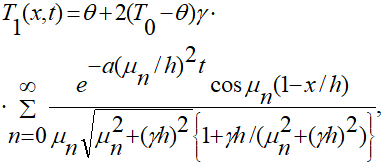(3.2)

где μ_n являются корнями уравнения:

(3.3)

Выражение (3.2) описывает температурное поле в упругом слое, возникающее за счет конвективного теплообмена с конденсатом облучаемой поверхности.

Температурное поле в упругом слое, возникающее за счет облучения, описывается функцией Т₂(х,t), для которой можно получить [1] выражение:

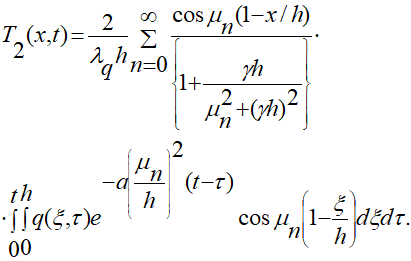(3.4)

Для определения распределения динамических напряжений в упругом слое к постановке начально-краевой задачи (1.4) — (1.7) добавляется краевое условие на второй границе при х = h [1]:

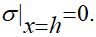(3.5)

Тогда для нахождения напряжения в слое получается начально-краевая задача (1.4) — (1.7), (3.5) с краевыми условиями первого рода. Ее решение получают [1] в виде:

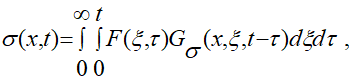(3.6)

где функция Грина соответствующей задачи (1.4) — (1.7), (3.5) определяется выражением:

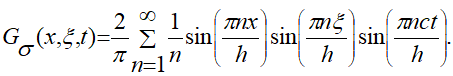(3.7)

В формулу (3.6) включается функция F, вычисляемая по формуле (1.5) с учетом найденного температурного поля (1.9), определяемого выражениями (3.2) и (3.4).

При получении разработанного вещественного решения в аналитическом виде уравнения (1.1) с постоянными теплофизическими характеристиками предлагаемый вариант решения оговариваемой начально-краевой задачи распространения тепла с фиксированным тепловым источником 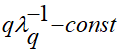, краевыми условиями (1.2), (1.3) с учетом граничного условия теплоизоляции для упругого слоя:

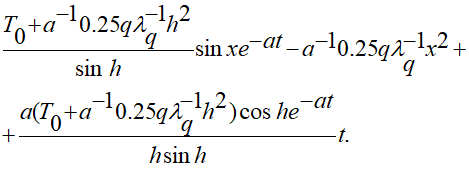(3.8)

Уравнение распределения динамических напряжений в упругом слое исследуется таким:

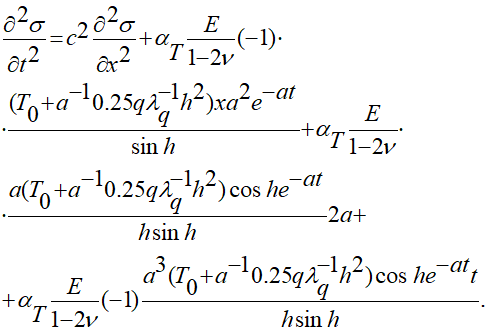(3.9)

Для определения динамических напряжений в упругом слое к начально-краевой задаче (3.9), (1.5), (1.6), (1.7) добавляется краевое условие (3.5).

Вариант вещественного решения такой задачи в аналитическом виде предлагается разработанным так:

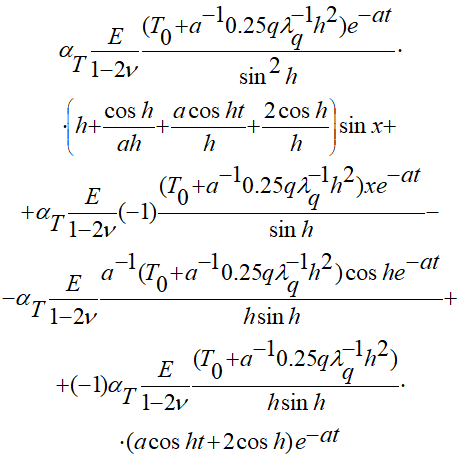(3.10)

При выполнении системы записанных соотношений вида:

(3.11)

возможный вариант решения в аналитическом виде оговариваемой задачи распределения динамических напряжений в упругом слое предлагается сформированным так:

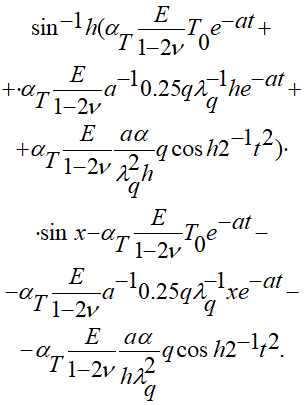(3.12)

Вариант вещественного уравнения распределения динамических напряжений в упругом слое с детерминированным тепловым источником вида 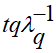предлагается таким:

(3.13)

Возможный вариант действительного решения в аналитическом виде искомой начально-краевой задачи (3.13), (1.5), (1.6), (1.7) с вещественным краевым условием (3.5) предлагается сформированным так:

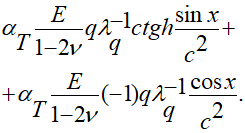(3.14)

Литература

[1]   Блажевич, С. В. Моделирование распределения тепловых напряжений под действием облучения с учетом конвективного теплообмена [Текст] / С. В. Блажевич, С. Н. Немцов, С. Е. Савотченко // Компьютерное моделирование электромагнитных процессов в физических, химических и технических системах : материалы седьмой научной конференции ДЭМП – 7, включающие состоявшийся V Международный семинар., (Воронеж 26-27 мая 2007), ГОУ ВПО ВГТУ 2007, С.200–206.

[2]   Харченко М.Э., Дорохов В.А., Колесников М.И. Оценка влияния структурных особенностей кристалла на стойкость ДМОП транзисторов к ионизирующему излучению // Моделирование систем и процессов. – 2022. – Т. 15, № 3. – С. 128-136.

[3]   Полуэктов А.В. Моделирование ослабления ионизируюшего излучения за счет защитного корпуса микросхем / Полуэктов А.В., Медведев Р.Ю., Заревич А.И. // Моделирование систем и процессов. 2024. Т. 17. № 2. С. 93-100.

[4]   Романов Д.В. Математическое моделирования зарождения солнечных пятен на фотосферном уровне солнца / Романов Д.В., Романов К.В., Романов В.А., Степанов Е.А., Лебедев А.А. // Вестник Самарского государственного технического университета. Серия: Физико-математические науки. 2023. Т. 27. № 4. С. 723-736.

[5]   Рогалев А.А.Оценивание множеств решений линейных систем обыкновенных дифференциальных уравнений с возмущениями на основе оператора коши /Рогалев А.А. // Вестник Самарского государственного технического университета. Серия: Физико-математические науки. 2023. Т. 27. № 2. С. 357-374.

References

[1] Blazhevich, S. V. Modeling of thermal stress distribution under irradiation with account for convective heat transfer [Text] / S. V. Blazhevich, S. N. Nemtsov, S. E. Savotchenko // Computer modeling of electromagnetic processes in physical, chemical and technical systems: materials of the seventh scientific conference DEMP – 7, including the V International seminar, (Voronezh May 26-27, 2007), GOU VPO VSTU 2007, pp. 200–206.

[2] Kharchenko M.E., Dorokhov V.A., Kolesnikov M.I. Assessment of the influence of structural features of a crystal on the resistance of DMOS transistors to ionizing radiation // Modeling of systems and processes. – 2022. – Vol. 15, No. 3. – pp. 128-136.

[3] Poluektov A.V. Modeling of ionizing radiation attenuation due to protective casing of microcircuits / Poluektov A.V., Medvedev R.Yu., Zarevich A.I. // Modeling of systems and processes. 2024. Vol. 17. No. 2. pp. 93-100.

[4] Romanov D.V. Mathematical modeling of sunspot formation at the photospheric level of the sun / Romanov D.V., Romanov K.V., Romanov V.A., Stepanov E.A., Lebedev A.A. // Bulletin of Samara State Technical University. Series: Physical and Mathematical Sciences. 2023. Vol. 27. No. 4. pp. 723-736.

[5] Rogalev A.A. Estimation of solution sets for linear systems of ordinary differential equations with perturbations based on the Cauchy operator / Rogalev A.A. // Bulletin of Samara State Technical University. Series: Physical and Mathematical Sciences. 2023. Vol. 27. No. 2. pp. 357-374.